In generating predictions about the future, one of the mechanical mathematical operations we often use is simple linear extrapolation. This approach is very elegant, very conservative, and is broadly applicable to a myriad of forecasting situations involving relative (differing) rates of growth. For example, if we are attempting to project what our company's gross profit margin on sales will be in three years, we might collect historical data about our price per unit sold (one variable) and about our direct cost per unit sold (the other variable).
Based upon prior data, we might determine either an average or anticipated rate of growth per year in each of these two "competing" variables. If we simply graph the respective rates of growth in each of these two competitive variables (usually I prefer to use a compound interest growth formula) we can see the difference between the two at any given time by superimposing the graphs.
For an example of this, you might wish to visit my Braintenance Blog post, located at:
http://braintenance.blogspot.com/2011/09/real-economics-lesson-growth-rates.html .
Simply hit the "BACK" button on your browser to return when you've finished.
The reason that this growth rate extrapolation so useful is its simplicity in terms of citing and illustrating trends involving two or more variables. Generally speaking, the greater the difference in annual growth rates, and the greater the passage of time, the larger will be the gap between the two. In some situations the two lines will eventually converge and cross each other -- in others, the two distance between the two lines at any given point on one axis will simply continue to increase, and never converge.
If we now enjoy a gross profit margin of 30% (for illustrative purposes), but our price per unit can only be increased by 3% annually due to competitive or economic concerns while our direct materials supplier is one of the only sources of supply accessible to us, and that company has been consistently (despite our pleas for mercy, and our whining about college tuition for the kids, confiding about Aunt Tillie's desperately-needed life saving surgery, sharing our worst fears about how we'll soon actually be losing money on our sales of our principal product, and the like) raising costs at an average of 7.5% annually, we can estimate the amount of decrease in our margin at any given time in the future during the forecast timeframe, and we can even determine at what point our gross profit margin will simply be too small to continue our manufacturing and sales of that particular product.
The notion and application of differential growth rates is one of the most crucial steps to making any predictive analysis.
This type of procedure is incredibly simple -- the greatest challenge to the prognosticator is determining which growth rates are most appropriate [and sadly, in the real world, they are seldom linear], while the greatest challenges to leadership and management are to monitor these changes and to prepare an actionable agenda to prevent the fulfillment of these prophesies.
In The Global Futurist, we paint scenarios of the future if trends or tendencies are permitted to continue along their current paths. A proactive strategist can change the future by his or her early intervention. Free will and the prospect of precipitous action are the "Human Factor Wild Cards" that can alter the sequence and path of events that lead to the future. The future is never certain, as long as 1) forecasting is not an exacting science, and as long as 2) Human Beings can choose to act upon their expectations of the future and take the initiative to change outcomes.
Douglas E Castle [http://www.linkedin.com/in/douglascastle]
http://SendingSignals.blogspot.com



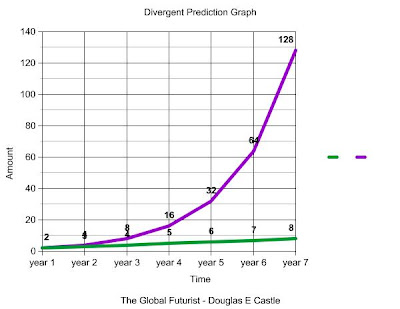

Linear extrapolation might work sometimes in, say, climatology. It's not going to predict the future worth a hill of beans, though. It completely misses any revolutionary new development-- by its very nature! Even besides that, it has a bad habit of ignoring holding capacities (say), and predicting (e.g.) that a sample of bacteria will rapidly fill up the entire universe.
ReplyDelete